Was ist das richtige Resultat?
6 ÷ 2 (1+2) =
- 9 – ist doch logisch50%
- 1 – seid ihr denn alle blöd????!!!46%
- Mir egal, Mathe ist eh doof5%
Der Wettbewerb ist inzwischen beendet.

Leute, die sich online wegen jedem Gugus anpöbeln, sind nichts Neues. Dass eine Diskussion über ein mathematisches Problem Tausende Kommentare generiert, hingegen schon. Nicht nur Menschen, sondern auch Taschenrechner kommen auf unterschiedliche Resultate. Woran liegt’s?
Ein mathematisches Problem geistert seit dem Jahr 2011 im Internet herum. Schon so lange streiten sich die Leute in Foren und alle wissen es besser. Aktuell ist das Problem einer mathematischen Gleichung wieder auf verschiedenen Online-Plattformen zu finden. In einem Thread auf Facebook haben sich über 1000 Personen wegen Mathe auf den Deckel gegeben.
Das Corpus delicti auf der Facebookseite Word Porn:
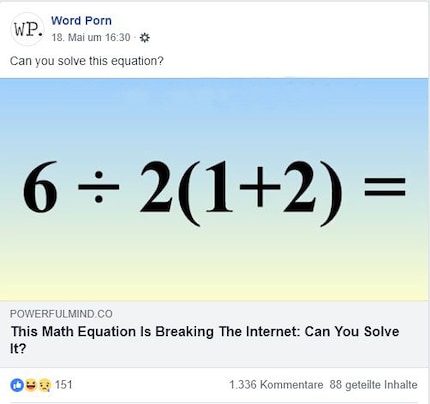
Die Gleichung 6÷2(1+2) scheint auf den ersten Blick ganz einfach zu sein. Sie beinhaltet eine Division, eine Multiplikation und eine Addition in Klammern. Die Klammer wird aufgelöst und das Resultat aus der Klammer multipliziert. So haben wir es alle in der Grundschule gelernt. Eigentlich. Denn so einfach ist’s eben doch nicht.
Während einige sagen, dass das Resultat 9 ist, sind sich andere sicher, dass die Gleichung 1 ergibt.
6 ÷ 2 (1+2) =
Der Wettbewerb ist inzwischen beendet.
Eigentlich hat eine simple Gleichung wie diese nur ein Resultat. Hier lässt sich aber darüber streiten. Das Problem ist die Notation, die je nach angewendeten Notations-Regeln zu einem unterschiedlichen Resultat führt. Klar ist, die Gleichung lässt sich wie folgt umschreiben:
6÷2(1+2)=6÷2(3)
Der Term in der Klammer muss zuerst ausgerechnet werden.
Aber dann kann die Gleichung auf zwei verschiedene Arten weiter umgeschrieben werden: Entweder (6÷2)×3=9 oder 6÷(2×3)=1
In der ersten Gleichung wird zuerst die Division durchgeführt, in der zweiten zuerst die Multiplikation. Die meisten Leute – und auch die meisten Taschenrechner – lösen die Gleichung von links nach rechts. Das ergibt die Lösung 9. Es gibt aber gewisse Notations-Regeln, unter deren Anwendung diese Lösung falsch ist. Der Prozess der Anwendung von Notationsregeln heisst Parsing. Ein Parser interpretiert, vereinfacht gesagt, eine Zeichenfolge.
Die Notation der Gleichung ist mehrdeutig. Sie ist entweder
(6÷2)×3=9 oder 6÷(2×3)=1. Es gibt zwei Interpretationen, die besagen, dass die zweite Notation, also das Resultat 1 richtig sind. Die erste beruht sich auf impliziter und expliziter Multiplikation.
In manchen Lehrbüchern hat die implizierte Multiplikation Vorrang:
Unter einer impliziten Multiplikation versteht man in der Mathematik die Notation 2(1+2), also die Notation ausgedrückt ohne Operator. Eine explizite Multiplikation wäre die Notation 2×(1+2).
Das heisst, es muss 6÷(2×3)=1 gerechnet werden. Wenn also diese Parsing-Regel angewendet wird, dann ist das Ergebnis 1. Die Regelung ist aber nur in einigen und nicht in allen algebraischen Lehrbüchern zu finden.
Auch einige Rechner wenden beim Parsen – also Interpretieren – der Gleichung diese Regel an. Andere hingegen nicht. Sogar Rechner derselben Hersteller rechnen unterschiedlich.

Bild: devrant.com
Es liegt aber nicht etwa an der Marke Casio. Auch die Rechner von Texas Instruments kommen nicht auf dasselbe Resultat. Die Modelle TI-80, TI-81, TI-82 und TI-85 sind so programmiert, dass sie der implizierten Multiplikation Vorrang geben. Die Modelle TI-83, TI-84 Plus, TI-89, TI-92 hingegen nicht, mit ihnen kommst du auf das Resultat 9.

Der TI-82 und der TI-83 Plus sind sich nicht einig.
Mit den Interpretationen der impliziten und expliziten Multiplikation ist das Problem leider noch nicht vom Tisch. Denn eine Division kann mit unterschiedlicher Notation dargestellt werden. Es gibt den Obelus ÷ und den Schrägstrich /. In der Vergangenheit wurde die mit ÷ bezeichnete Division anders behandelt als die mit / bezeichnete. Anstatt Divisionen und Multiplikationen von links nach rechts auszuwerten, würde ÷ darauf hinweisen, dass alles links davon durch alles rechts davon geteilt werden sollte. Du kannst dir das auch so vorstellen, wie wenn du alles auf einem Bruchstrich notieren würdest.
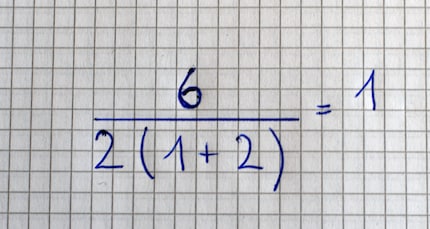
Mit dem Obelus, also so wie die Gleichung in den Foren gestellt wird, wäre das Ergebnis auch wieder 1. Aber keine der oben genannten Regeln ist weit verbreitet und auch nicht generell akzeptiert.
Mathe abschaffen
. Das Internet wird wohl noch lange über die korrekte Lösung streiten. Dabei liegt nur jemand falsch. Nämlich die Person, die die Gleichung formuliert hat. Warum das?
Der Zweck einer mathematischen Notation ist es, eindeutig zu sein, so dass sie von allen gleich interpretiert wird – dies ist hier eindeutig nicht der Fall. Der Gleichung müsste eine Art Gebrauchsanweisung beiliegen.
Experimentieren und Neues entdecken gehört zu meinen Leidenschaften. Manchmal läuft dabei etwas nicht wie es soll und im schlimmsten Fall geht etwas kaputt. Ansonsten bin ich seriensüchtig und kann deshalb nicht mehr auf Netflix verzichten. Im Sommer findet man mich aber draussen an der Sonne – am See oder an einem Musikfestival.
Interessantes aus der Welt der Produkte, Blicke hinter die Kulissen von Herstellern und Portraits von interessanten Menschen.
Alle anzeigen